Question

A person's body is covered with 1.69 m^2 of wool clothing. The thickness of the wool is 1.87 × 10^-3 m. The temperature at the outside surface of the wool is 13.9 °C, and the skin temperature is 35.4 °C. How much heat per second does the person lose due to conduction?

Answer 1

The concept required to solve this problem is related to heat conductivity as a function of time.

Mathematically in a stable state the heat flux is constant and its rate of change as a function of time can be described under the function

`(Q)/(t) = (kA\Delta T)/(d)`

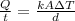
Where

k= Coefficient of thermal conductivity

A = Area of the object

`\Delta T` =Temperature difference across object

d= thickness of object

According to the values given we have then,

`k_(wool) = 0.04W/mK`

`\Delta T = 35.4-13.9`

`d = 1.87*10^(-3)m`

`A = 1.69m^2`

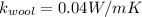
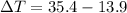
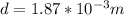
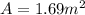
Replacing we have,

`(Q)/(t) = ((0.04)(1.69)(35.4-13.9))/(1.87*10^(-3))`

`(Q)/(t) = 777.21J/s`

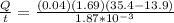
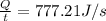
Therefore the quantity of heat per second does the person lose due to conduction is 777.21J/s