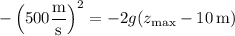Question

A small rocket is fired from a launch pad 10 m above the ground with an initial velocity left angle 250 comma 450 comma 500 right angle ​m/s. A cross wind blowing to the north produces an acceleration of the rocket of 2.5 m divided by s squared. Assume the​ x-axis points​ east, the​ y-axis points​ north, the positive​ z-axis is vertical​ (opposite g), and the ground is horizontal. Answer parts a through d.

Find:
a/ Velocity and position vectors.b/ Determine the time of the flight and range of the rocketc/ Determine the maximum hight of the rocket.

Answer 1

Let
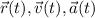`\vec r(t),\vec v(t),\vec a(t)` denote the rocket's position, velocity, and acceleration vectors at time
`t`.

We're given its initial position

`\vec r(0)=\langle0,0,10\rangle\,\mathrm m`

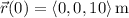
and velocity

`\vec v(0)=\langle250,450,500\rangle(\rm m)/(\rm s)`

Immediately after launch, the rocket is subject to gravity, so its acceleration is

`\vec a(t)=\langle0,2.5,-g\rangle(\rm m)/(\mathrm s^2)`

where
`g=9.8(\rm m)/(\mathrm s^2)`.

a. We can obtain the velocity and position vectors by respectively integrating the acceleration and velocity functions. By the fundamental theorem of calculus,

`\vec v(t)=\left(\vec v(0)+\displaystyle\int_0^t\vec a(u)\,\mathrm du\right)(\rm m)/(\rm s)`

`\vec v(t)=\left(\langle250,450,500\rangle+\langle0,2.5u,-gu\rangle\bigg|_0^t\right)(\rm m)/(\rm s)`

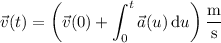
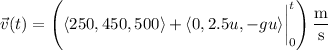
(the integral of 0 is a constant, but it ultimately doesn't matter in this case)

`\boxed{\vec v(t)=\langle250,450+2.5t,500-gt\rangle(\rm m)/(\rm s)}`

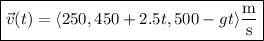
and

`\vec r(t)=\left(\vec r(0)+\displaystyle\int_0^t\vec v(u)\,\mathrm du\right)\,\rm m`

`\vec r(t)=\left(\langle0,0,10\rangle+\left\langle250u,450u+1.25u^2,500u-\frac g2u^2\right\rangle\bigg|_0^t\right)\,\rm m`

`\boxed{\vec r(t)=\left\langle250t,450t+1.25t^2,10+500t-\frac g2t^2\right\rangle\,\rm m}`

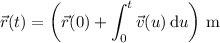
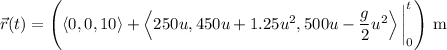
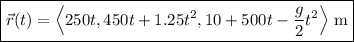
b. The rocket stays in the air for as long as it takes until
`z=0`, where
`z` is the
`z`-component of the position vector.

`10+500t-\frac g2t^2=0\implies t\approx102\,\rm s`

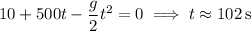
The range of the rocket is the distance between the rocket's final position and the origin (0, 0, 0):

`\boxed\`

c. The rocket reaches its maximum height when its vertical velocity (the
`z`-component) is 0, at which point we have

`-\left(500(\rm m)/(\rm s)\right)^2=-2g(z_(\rm max)-10\,\mathrm m)`

`\implies\boxed{z_(\rm max)=125,010\,\rm m}`