Question

A bike messenger is standing by the road when he sees a dog running towards him at 4 ft per second The bike messenger takes off, and his acceleration for the first fifteen seconds is 2/5 feet per second per second.

(a) Write an equation describing the instantaneous change in the distance between the dog and the messenger, as a function of time, assuming the messenger is fleeing the dog
(b) Assuming the messenger notices the dog in time to get away, after how many seconds is the dog closest to the messenger.
(c) Write an equation for the distance between the dog and the messenger, if the messenger takes off when the dog is twenty-five feet away. Will the dog catch the messenger, and if so, when? Hint: Graph it if you need to. Also, what happens if you use the quadratic formula, and wind up with imaginary roots?
(d) Write that same equation if the dog and the messenger are fifteen feet away when the messenger takes off. Will the dog catch the messenger, and if when? so,
(e) Find the maximum starting distance between the dog and the messenger, so that the dog catches the messenger. Hint: Solve the discriminant for zero.

Answer 1

a) The change in distance is f'(t) = 0.4t - 4 feets

b) After 10 seconds the dog gets the closest to the messenger.

c) f(t) = 0.2t² - 4t + 25

The dog doesnt catch the messenger, the quadratic formula has imaginary roots, that means that the distance function is always positive because it cant take negative values due to Bolzano's Theorem.

d) f(t) = 0.t²-4t+15. The dog catches the messenger in 5 seconds

e) The maximun starting distance is 20 feets.

Explanation:

Dog speed = 4 f/s

biker initial speed = 0 f/s (b'(0) = 0)

biker acceleration = 0.4 f/s²

Hence, biker speed is b'(t) = 0.4t f/s (it depends on the transcurred time)

The distance between the biker and the dog con be computed as follows:

f(t) = d0 + b(t) - d(t)

Where t is the amount of seconds passed, d0 is the initial distance, b(t) is the distance the biker traveled since he start fleeing and d(t) is the dog distance.

a) The instantaneous change in distance is

f'(t) = b'(t) - d'(t) = 0.4t - 4

b) Note that the instantaneous change in distance is a positive slope linear function, so it will start beign negative and then it will be positive. The dog will be approaching until f'(t) = 0, then the distance will grow bigger. So the dog got the closest to the messenger when f'(t) = 0, as a result

0.4t - 4 = 0 ⇒ t = 10

After 10 seconds the dog gets the closest to the messenger.

c) we assume that f(0) = d0 = 25.

Since b(0) = 0 and b'(t) = 0.4t, then b(t) is 0.2t², and since d'(t) = 4, then d(t) = 4t. We can conclude that

f(t) = 25+ 0.2t² - 4t = 0.2t² - 4t + 25

Note that this distance function applies as long as the dog didnt catch the messenger. The dog will catch the messenger as soon as a zero is encountered. In order to find a zero, we use the quadratic formula

`r_o, \, r_1 = (4 \, ^+_- √((-4)^2-4*0.2*25) )/(2*0.2)`

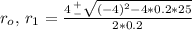
Inside the square root we have 16-20 = -4, so it doesnt have roots. This means that the function wont have zeros, so it will be always positive. The dog doesnt catch the messenger.

d) Here we take f replacing the constant value by 15 instead of 25. So f(t) = 0.t²-4t+15. And the quadratic formula is

`r_0, r_1 = (4 \, ^+_- \sqrt((-4)^2 - 4*0.2*15))/(2*0.2) = (4 \, ^+_- \sqrt 4)/(0.4)`

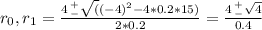
Here the discriminant is positive, so the dog will cath the messenger eventually. The lowest root is
`(4 -2)/(0.4) = 5`

Hence, after 5 seconds, the dogs catches the messenger.

e) To maximixe the distance, we should take a constant value high enough so that it is the maximun constant value such that the discriminant is non negative. Thus we equals the discriminant to zero.

The discriminant is (-4)² - 4*0.2*D = 16-0.8D, where D is the initial distance. We equal that expresion to 0, therefore

0 = 16-0.8D ⇒ D = 16/0.8 = 20.

The maximun starting distance we can take is 20. For that distance, the dog will catch the biker in 4/0.4 = 10 seconds.