Question

Consider a basketball player spinning a ball on the tip of a finger. If a player performs 1.99 J of work to set the ball spinning from rest, at what angular speed ω will the ball rotate? Model a basketball as a thin-walled hollow sphere. For a men's basketball, the ball has a circumference of 0.749 m and a mass of 0.624 kg .

Answer 1

To solve this problem it is necessary to apply the concepts related to rotational kinetic energy, the definition of the moment of inertia for a sphere and the obtaining of the radius through the circumference. Mathematically kinetic energy can be given as:

`KE= I\omega^2`

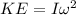
Where,

I = Moment of inertia

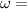`\omega =` Angular velocity

According to the information given we have that the radius is

`\Phi= 2\pi r`

`0.749m = 2\pi r`

`r = 0.1192m`

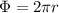
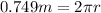
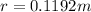
With the radius obtained we can calculate the moment of inertia which is

`I = (2)/(3)mr^2`

`I = (2)/(3)(0.624)(0.1192)^2`

`I = 5.91*10^(-3) kg \cdot m^2`

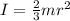
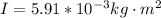
Finally, from the energy equation and rearranging the expression to obtain the angular velocity we have to

`\omega = \sqrt{(2KE)/(I)}`

`\omega = \sqrt{(2(1.99))/(5.91*10^(-3))}`

`\omega = 25.95rad/s`

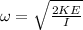
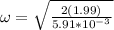
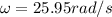
Therefore the angular speed will the ball rotate is 25.95rad/s