Question

For a first-order reaction, the half-life is constant. It depends only on the rate constant and not on the reactant concentration. It is expressed as: t1/2=0.693/k

For a second-order reaction, the half-life depends on the rate constant and the concentration of the reactant and so is expressed as: t1/2= 1/k[A]0
A. A certain first-order reaction (A-->Products) has a rate constant of 3.30×10^-3 s^-1 at 45 degrees C. How many minutes does it take for the concentration of the reactant, [A], to drop to 6.25% of the original concentration?
B. A certain second-order reaction (B-->Products) has a rate constant of 1.70×10^-3 M^-1*s^-1 at 27 degrees C and an initial half-life of 296 s. What is the concentration of the reactant B after one half-life?

Answer 1

A. 14 min

B . 0.995 M

Step-by-step explanation:

A.

Using integrated rate law for first order kinetics as:

`[A_t]=[A_0]e^(-kt)`

Where,

`[A_t]` is the concentration at time t

`[A_0]` is the initial concentration

Given:

The final concentration is dropped to 6.25 % of the initial concentration. SO,

`\frac {[A_t]}{[A_0]}` = 0.0625

k =
`3.30* 10^(-3)\ s^(-1)`

So,

`\frac {[A_t]}{[A_0]}=e^(-k* t)`

`0.0625=e^{-3.30* 10^(-3)* t}`

`\ln \left(0.0625\right)=\ln \left(e^{-3.3* \:10^(-3)t}\right)`

`\ln \left(0.0625\right)=-3.3* \:10^(-3)t`

`t=840.18\ s`

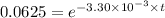
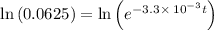
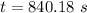
Also, 1 s = 1/60 minutes.

So,
`t=(840.18)/(60)=14\ min`

14 minutes it takes for the concentration of the reactant to drop to 6.25% of the original concentration.

B.

(a) Half life expression for second order kinetic is:

`t_(1/2)=(1)/(k[A_o])`

Where,

`[A_o]` is the initial concentration = ?

k is the rate constant =
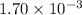`1.70* 10^(-3)` M⁻¹s⁻¹

Half life = 296 s

So,

`296=(1)/(1.70* 10^(-3)* [A_o])`

`296=(1000)/(1.7[A_o])`

`[A_o]=(1250)/(629)`

`[A_o]=1.99\ M`

Half life is the time at which the concentration of the reactant reduced to half. So, concentration remains =
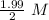`(1.99)/(2)\ M` = 0.995 M