Answer:
a)
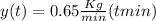
b)
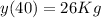
Explanation:
Data
Brine a (Ba)

Brine b (Bb)
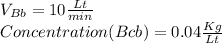
we have that per every minute the amount of solution that enters the tank is the same as the one that leaves the tank (15 Lt / min)
, then the amount of salt (y) left in the tank after (t) minutes:
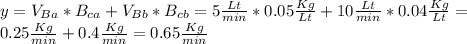
Finally:
a)
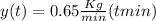
b)

being y(t) the amount of salt (y) per unit of time (t)