Question

A mass M slides upward along a rough plane surface inclined at angle θ= 0.21 in radians to the horizontal. Initially the mass has a speed Vo = 2.13 m/s, before it slides a distance L = 1.0 m up the incline. After sliding this distance the new speed of the mass isVo/ 3 measured in m/s. What is the acceleration of the sliding mass?

Answer 1

I made a diagram of the problem according to the description given. In order not to go into details of the components, I also define the coordinate diagram parallel to the inclined plane and not at the given angle.

To solve the problem it is necessary to apply the kinematic equations of motion in which time is excluded to determine the speed, acceleration or position of the bodies.

Mathematically this is given by

`V_2^2-V_1^2 = 2ax`

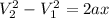
Where

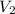`V_2` = Final velocity

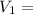`V_1 =` Initial velocity

a = Acceleration

x = Diplacement

According to the information given one third of the final speed is equivalent to the initial speed, therefore,

`(V_1)/(3)^2-V_1^2 = 2a(1)`

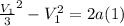
Re-arrange to find the acceleration

`a = -(4)/(9)(V_1)^2`

`a = -(4)/(9)* 2.13^2`

`a = -2.0164m/s^2`

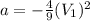
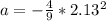
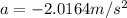
Negative denotes acceleration down the incline.