Question

A researchers wants to determine the mean weight of avocados grown in Southern California. The population from which the sample is drawn is such that the weight of the avocados is approximately normally distributed for the sample. The size of the sample is 9, the sample mean determined from this sample is 6 ounces, and the sample standard deviation determined from this sample is 0.75 ounces. Help the researcher by determining the 90% confidence interval for the true mean weight of these Southern California avocados. (This problem will be solved after lecture on confidence intervals.)

Answer 1

Answer: (0.465, 5.535)

Explanation:

Formula to calculate the confidence interval (when population standard deviation is unknown) is given by :-

`\overline{x}\pm t_(\alpha/2) (s)/(√(n))`

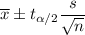
, where
`\overline{x}` = sample mean.

s= sample standard deviation.

n= Sample size.

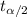`t_(\alpha/2)` = critical value

By considering the given information , we have

`\overline{x}=6`

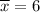
s=0.75

n= 9

Significance level =
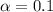`\alpha=0.1` [1-0.90=0.1]

By using students' t distribution -table , the critical value for 95% confidence level :

`t_(\alpha/2 , n-1)=t_(0.1/2,\ 8)=1.86`

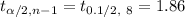
[Note: degree of freedom = n-1]

Now, the 90% confidence interval for the true mean weight of these Southern California avocados will be :

`6\pm (1.86) (0.75)/(√(9))`

`6\pm (1.86) (0.75)/(3)`

`6\pm (1.86) 0.25`

`6\pm 0.465=(6-0.465,\ 6+0.465)=(0.465,\ 5.535)`

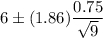
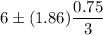
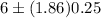
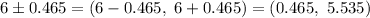
Hence, the required confidence interval =(0.465, 5.535)