Answer: 84.84cm
Explanation:
Since the vertices of the square touches the circle , it means that the diameter of the circle is the same as the diagonal of the square.
Diameter of a circle , given the radius = 2 x radius
Diameter of the circle is therefore 2 x 15 = 30cm
Recall that in a square the point where the diagonals intersect , divides each diagonal into two equal parts , and since the square touches the edge of the circle , it means that the length of the diagonal is 30.
We need to find the length of one side of the square , in order to find the perimeter . That means we will use Pythagoras rule, which states that the square on the hypotenuse of a right-angled triangle is equal in area to the sum of the squares on the other two sides.
The hypotenuse is the unknown side ,let it be x and the other sides are 15 and 15
Therefore :
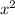 =
=
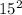 +
+
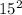
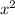 = 225 + 225
= 225 + 225
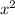 = 450
= 450
x =
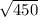
x ≈21.21
Therefore , the side of the square is 21.21
The formula for calculating the perimeter of a square is 4x,
Therefore : P = 4(21.21)
P = 84.84 cm