Answer:
Statement (1) is sufficient.
Statement (2) is not sufficient.
Explanation:
Consider we need to find check whether the given statements are sufficient or not.
The standard form of a circle is
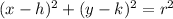
where, (h,k) is center and r is the radius.
The center of the circle is (0,0). So, the equation of circle is
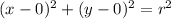
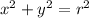
Statement (1) : The radius of the circle is 4.
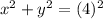
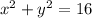
The sum of the squares of the coordinates of P is 16. So statement (1) is sufficient.
Statement (2) : The sum of the coordinates of P is 0.
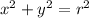
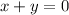
We can not solve these two equation because radius is not given.
Therefore, the statement (2) is not sufficient.