Question

A particular conductor has 3.0 × 10^27 mobile electrons per cubic meter. The material is in the shape of a cylinder of length 6.0 cm and diameter 1.0 cm. When the bar is connected to a battery with an emf of 2.5 V, a current of 5.0 mA begins to flow.

What is the resistivity of the bar?

Answer 1

0.654 ohm - metre

Step-by-step explanation:

length, l = 6 cm

diameter, d = 1 cm

radius, r = 0.5 cm

Voltage, V = 2.5 V

current, i = 5 mA

According to Ohm's law

V = i x R

2.5 = 0.005 x R

R = 500 ohm

Let ρ be the resistivity of material of conductor.

Let A be the area of crossection of the conductor.

A = πr²

A = 3.14 x 0.005 x 0.005 = 7.85 x 10^-5 m^2

`\rho =(R* A)/(l)`

`\rho =(500* 7.85* 10^(-5))/(0.06)`

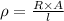
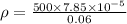
ρ = 0.654 ohm - metre

Answer 2

Step-by-step explanation:

Given

Length of cylinder
`L=6 cm`

diameter of cylinder
`d=1 cm`

Area of cross-section
`A=(\pi* d^2)/(4)`

`A=(\pi * 10^(-4))/(4)=7.855* 10^(-5) m^2`

`Emf =2.5 V`

current
`I=5 mA`

`Resistance=(V)/(I)=(2.5)/(5* 10^(-3))`

`R=500 \Omega`

R is also given by

`R=\rho (L)/(A)`

where
`\rho =resistivity`

`\rho =(RA)/(L)=(500* 7.85* 10^(-3))/(6)`

`\rho =0.654 \Omega -m`