Question

A park ranger wanted to measure the height of a tall tree. The range stood 9.50 m from the base of the tree; and he observed that his line of sight made an angle of 65.2° above the horizontal as he looked at the top of the tree. The park ranger's eyes are 1.80 m above the ground. What is the height of the tree?

Answer 1

22.35 m

Explanation:

Hello , I can help you with this.

Step 1

define a right triangle

height of the three: H

opposite side=

the height of the tree - 1.8 m as the horizontal should be at the height of the guard's eyes

opposite side=

H-1.8

adjacent side=distance between the guard and the tree= 9.5 m

adjacent side= 9.5 m

Hypotenuse=distance between ranger's eyes and the top of the three=C

Hypotenuse=C

α=angle between the hypotenuse and the adjacent side =65.2°

α=65.2°

Step 2

find the value of the hypotenuse with the cosine function

`cos\alpha =(op.side)/(hypotenuse)`

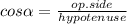
put the values into the equation and solve for hypotenuse

`cos\ 65.2 =(9.5\ m)/(hypotenuse) \\Hypotenuse=(9.5\ m)/(cos\ 65.2 ) \\Hypotenuse=(9.5\ m)/(0.41)\\Hypotenuse=22.64\ m`

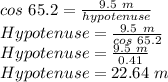
Step 3

find the value of the opposite side using the Pythagorean theorem

T.P

`hypotenuse^(2)=adj.sede^(2)+opp.side^(2)`

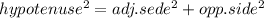
solve for op.side and put the values into the equation

`hypotenuse^(2)=adj.sede^(2)+opp.side^(2)\\hypotenuse^(2)-adj.sede^(2)=opp.side^(2)\\\\sqrt{hypotenuse^(2)-adj.sede^(2)} =opp.side\\opp.side=\sqrt{22.64^(2)-9.5^(2)} \\opp.side=√(422.3196)}\\op.side=20.55 m`

Step 4

use the equation opposite side=

H-1.8 to find H ( height of the three)

opposite side=

H-1.8

20.55=H-1.8

add 1.8 in both sides

20.55+1.8=H-1.8+1.8

H=22.35 m

Have a great day.