Answer:
Roland is right, he can be 95% sure that average gas prices have gone up since the same time last year.
Explanation:
Let μ be average gas price around Syracuse.
Then hypotheses are:
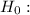 μ = $2.68
μ = $2.68
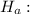 μ > $2.68
μ > $2.68
Then test statistic can be calculated as:
z=
 where
where
- X is the Roland's calculated average gas prices of 50 gas stations ($2.74)
- M is the average average gas prices in the entire of Syracuse last year
- s is the standard deviation ($0.11)
Then z=
 ≈ 3.86
≈ 3.86
Since P-value of test statistic ≈ 0.00006 <0.05 (significance level), we can reject the null hypothesis.