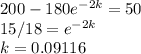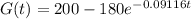Answer:
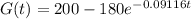
Explanation:
Given that a disease is spreading through a herd of 200 goats. Let G(t) be the number of goats who have the disease t days after the outbreak. The disease is spreading at a rate proportional to the number of goats who do not have the disease. Suppose that 20 goats had the disease initially and 50 goats have the disease after 2 weeks.
a) i.e.
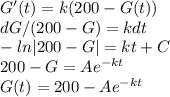
Initially
b)
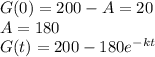
c) G(2) =50