Question

A financier plans to invest up to $600,000 in two projects. Project A yields a return of 8% on the investment, whereas project B yields a return of 16% on the investment. Because the investment in project B is riskier than the investment in project A, she has decided that the investment in project B should not exceed 35% of the total investment. How much should the financier invest in each project in order to maximize the return on her investment?

Answer 1

To maximize return, A with 390000 and B with 210000

Explanation:

Given that a financier plans to invest up to $600,000 in two projects

Let x be the amount invested in 8% and y in 16%

Other information given is the investment in project B is riskier than the investment in project A, she has decided that the investment in project B should not exceed 35% of the total investment.

i,.e.
`y\leq 0.35(600000)\\y\leq 210000`

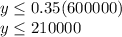
Also
`x+y = 600000`

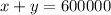
The objective is to maximize interest function

`Z=0.08x+0.16y`

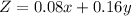
subject to the above two constraints.

The corner points would be P(390000,210000) or Q(600000,0)

Calculate Z for these two points

Profit at P =
`390000(0.08)+210000(0.16)\\= 64800`

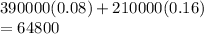
Profit at Q =
`600000(0.08)\\= 48000`

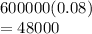
So to maximize return, A with 390000 and B with 210000