Question

A random sample of 160 car accidents are selected and categorized by the age of the driver determined to be at fault. The results are listed below. The age distribution of drivers for the given categories is 18% for the under 26 group, 39% for the 26-45 group, 31% for the 45-65 group, and 12% for the group over 65. Calculate the chi-square test statistic used to test the claim that all ages have crash rates proportional to their driving rates.

Age >26 26-45 46-65 45<

Drivers 66 39 25 30

A).95.431
B).101.324
C).85.123
D).75.101

Answer 1

D).75.101

Explanation:

Previous concepts

The Chi-Square test of independence is used "to determine if there is a significant relationship between two nominal (categorical) variables". And is defined with the following statistic:

`\chi^2 =\sum_(i=1)^n ((O-E)^2)/(E)`

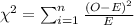
Where O represent the observed values and E the expected values.

State the null and alternative hypothesis

Null hypothesis: All ages have crash rates proportional to their driving rates

Alternative hypothesis: Not All ages have crash rates proportional to their driving rates

The observed values are given by the table given:

Age <26 26-45 46-65 >45

Drivers 66 39 25 30

Calculate the expected values

In order to calculate the expected values we can use the rates given by the problem:

The age distribution of drivers for the given categories is :

18% for the under 26 group, E1 = 160*0.18=28.8

39% for the 26-45 group, E2=160*0.39=62.4

31% for the 45-65 group, E3=160*0.31=49.6

12% for the group over 65. E4=160*0.12=19.2

Calculate the statistic

`\chi^2 =((66-28.8)^2)/(28.8)+((39-62.4)^2)/(62.4)+((25-49.6)^2)/(49.6)+((30-19.2)^2)/(19.2)`

`\chi^2 =75.101`

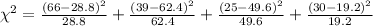
Calculate the critical value

First we need to calculate the degrees of freedom given by:

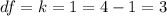`df= k=1=4-1= 3`, where k represent the total number of categories, for tis case k=4

We can use a confidence level for example 95%, and the significance would be
`\alpha=1-0.95=0.05` and we can find the critical value with the following excel code: "=CHISQ.INV(0.95,3)", and our critical value would be
`\chi^2_(crit)=7.815`

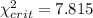
We can calculate also the p value:

`p_v =P(\chi^2_(3)>75.101)=0`

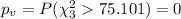
And we got the same decision reject the null hypothesis at 5% of significance.