Answer:
222.8 K
Step-by-step explanation:
length of cylinder, l = 20 cm = 0.2 m
diameter of cylinder = 3 cm
radius of cylinder, r = 1.5 cm = 0.015 m
Volume of air initially, V1 = πr²l
V1 = 3.14 x 0.015 x 0.015 x 0.2 = 1.413 x 10^-4 m^3
V2 = V1/2
P1 = 1 atm = 1.01 x 10^5 Pa
T1 = 21°C = 21 + 273 = 294 K
γ = 1.4
This is the adiabatic compression

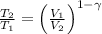
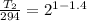
T2 = 222.8 K
Thus, the temperature of air is 222.8 K.