Answer:
a and c are true
Explanation:
The question is about diagonalizability of a matrix.
a) Given that A is a 13x17 matrix over R
We get
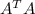 will be a square matrix 13x13.
will be a square matrix 13x13.
Being a square matrix this is diagonalizable provided eigen values are independent.
True
b) A 3 × 3 matrix A with only one eigenvalue cannot be diagonalizable.
False. For a square matrix to be diagonalizable, the eigen values should be independent.
c) A matrix A of size n×n is diagonalizable if and only if A has n distinct eigenvalues. g
This is true, because for a square matrix with distinct eigen values we can see that it is diagonalizable.