Question

The Wellbuilt Company produces two types of wood chippers, economy and deluxe. The deluxe model requires 3 hours to assemble and 1/2 hour to paint, and the economy model requires 2 hours to assemble and 1 hour to paint. The maximum number of assembly hours available is 24 per day, and the maximum number of painting hours available is 8 per day. If the profit on the deluxe model is $98 per unit and the profit on the economy model is $72 per unit, how many units of each model will maximize profit? deluxe units economy units?

Answer 1

The maximum profit is reached with 4 deluxe units and 6 economy units.

Explanation:

This is a linear programming problem.

We have to optimize a function (maximize profits). This function is given by:

`P=98D+72E`

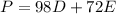
being D: number of deluxe units, and E: number of economy units.

The restrictions are:

- Assembly hours:
`3D+2E\leq24`

- Paint hours:
`0.5D+1E\leq8`

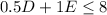
Also, both quantities have to be positive:

`D\geq 0\\\\E\geq0`

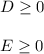
We can solve graphically, but we can evaluate the points (D,E) where 2 or more restrictions are saturated (we know that one of this points we will have the maximum profit)

`(8;0) \rightarrow  P=98*8+72*0= 784\\\\(0;8) \rightarrow P= 98*0+72*8=576\\\\(4;6) \rightarrow P=98*4+72*6=824`

The maximum profit is reached with 4 deluxe units and 6 economy units.