Question

The FSW bookstore has determined that their daily revenue has a population mean of $500 and a population standard deviation of $80. Assume that the daily revenue is normally distributed. If 1000 days were selected independently from this population then what would be the expected number of days for which the daily revenue is $400 or less?

Answer 1

Expected number of days for which the daily revenue is $400 or less is 105.6

Explanation:

Expected number of days for which the daily revenue is $400 or less can be written as

P(X<=400) where X is a variable in the distribution of daily revenue of the bookstore.

P(X<=400) = P(z<z*) where z* is the z-score of $400 in the distribution

z* can be calculated as:

z*=
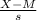`(X-M)/(s)` where

• X = $400

• M is the population mean of daily revenue ($500)

• s is the population standard deviation ($80)

Then z*=
`(400-500)/(80)` =-1.25

From this P(z<z*)≈0.1056

Finally, expected number of days for which the daily revenue is $400 or less in the selected 1000 days is 1000×0.1056=105.6