Question

On Jan 1, 2012, FIN307 is considering the newly issued 10-year AAA corporate bond, which is due Jan 1, 2022, with a coupon rate of 6% per year paid every 6 months. The bond is traded at par. Suppose the market interest rate declines by 100 bps (i.e., 1%), what is the duration (before interest rate change) and the effect of the market interest decline on the bond price? Hint: if your calculator does not have a build-in function for duration, please go to excel and do the calculation manually by setting up 6 columns for t (=1, 2, 3…..20), DF(discount factor or 1/PV factor), CF (cashflow), PV (present value of CF=CF*DF), w(weight=PV/sum of PV or P0), and t*w. Then sum up all t*w, then divide by 2 (because here coupon is paid semiannually).

Answer 1

DURATION: 15.52358724

Step-by-step explanation:

t // cash flow // pv // duration

1 30 $ 29.27 0.027151915

2 30 $ 28.55 0.052979346

3 30 $ 27.86 0.07753075

4 30 $ 27.18 0.100853008

5 30 $ 26.52 0.122991473

6 30 $ 25.87 0.143990017

7 30 $ 25.24 0.163891076

8 30 $ 24.62 0.182735695

9 30 $ 24.02 0.200563568

10 30 $ 23.44 0.217413081

11 30 $ 22.86 0.233321356

12 30 $ 22.31 0.248324281

13 30 $ 21.76 0.262456557

14 30 $ 21.23 0.27575173

15 30 $ 20.71 0.288242226

16 30 $ 20.21 0.29995939

17 30 $ 19.72 0.310933514

18 30 $ 19.23 0.321193874

19 30 $ 18.77 0.330768759

20 1030 $ 628.58 11.66253562

$ 1,077.95 15.52358724

There is 20 payment as the bond stands for 10 years and does 2 payment per year

payment per year:

1,000 x 6% / 2 = $ 30 interest payment

then, we have the maturity at year-end for $ 1,000

Then, for the PV we use the lump sum:

`(Cashflow)/((1 + rate)^(time) ) = PV`

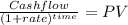
For last step we do the average for that and multiply by the payment number