Question

The quadratic function d= -4x+1,100 models a snowboarder's distance, in feet, from the bottom of a hill x seconds after the snowboarder starts moving down the hill. After how many seconds is the snowboarder 100 ft from the bottom of the hill?

Answer 1

16 seconds (Approximately)

Explanation:

Given:

The function that gives the distance of snowboarder from the bottom of hill with time 'x' is:

`d=-4x^2+1100`

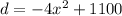
Final position of the snowboarder is
`d=100\ ft`

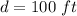
Now, plugging in 100 for 'd' and solving for 'x', we get:

`100=-4x^2+1100`

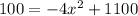
Adding -1100 both sides, we get:

`100-1100=-4x^2+1100-1100\\-1000=-4x^2`

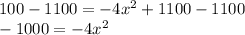
Dividing both sides by -4, we get:

`(4x^2)/(4)=(1000)/(4)\\x^2=250`

Taking square root and neglecting the negative root as time can't be negative. So,

`√(x^2)=√(250)\\x=5√(10)=15.8\ s\approx 16\ s`

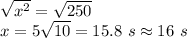
Therefore, after 16 seconds, the snowboarder will be at a distance of 100 ft from bottom of hill.