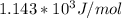Answer:
Step-by-step explanation:
Using the Arrhenius equation for the give problem:

Taking the natural log (ln) of both sides, we have:
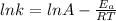
In the given problem, we have two rate constants at two different temperatures. Thus:
 (1)
(1)
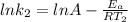 (2)
(2)
Subtracting equation (1) from equation (2), we have:
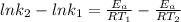 (3)
(3)
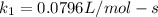 ;
;
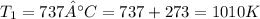
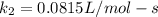 ;
;

Therefore, equation (3) becomes:
![ln 0.0815 - ln 0.0796 = E_(a)[(1)/(8.314*1010) - (1)/(8.314*1220)]](https://img.qammunity.org/2020/formulas/chemistry/college/4ji8wayqehicc6ljg5qt5sui5tvad6n53m.png)
-2.507 - (2.531) = Ea*[0.00012 - 0.000099]
Ea = 0.024/0.000021 = 1142.86 J/mol
The activation energy of the reaction in scientific notation is