Answer:
1. Option C
2. Option B
3. Option B
4. Option D
Explanation:
From the given graph it is clear that
PR = 6 units
QR = 4 units
TU = 2 units
SU = 3 units
Now,
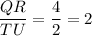
Hence, the correct option is C.
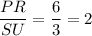
Hence, the correct option is B.
Using given information, we get
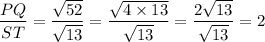
Hence, the correct option is B.
We conclude that all corresponding sides are proportional.
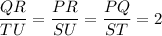
 (Using SSS similarity)
(Using SSS similarity)
Hence, the correct option is D.