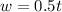Question

At time tequals​0, water begins to drip out of a pipe into an empty bucket. After 14 ​minutes, there are 7 inches of water in the bucket. Write a linear function rule to model how many inches of water w are in the bucket after any number of minutes t.

Answer 1

`w=0.5t`

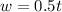
Explanation:

Given:

'w' represents inches of water left after 't' minutes of time.

The dripping out of water is a linear function.

At time 't' equal to 0, the bucket was empty.

After 14 minutes, there are 7 inches of water in the bucket.

A linear function model is of the form:
`w=mt+b`

`Where, m\to\textrm{dripping rate of water}\\b\to\textrm{water level at t=0}`

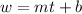
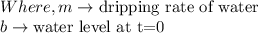
Now, at
`t=0,w=0(\textrm{As bucket was empty})`

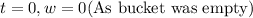
At
`t=14,w=7`

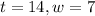
Therefore, plugging these values in the above linear model and solving the system of linear equations. This gives,

`0=m(0)+b\\0=0+b\\b=0\\\\7=14m+0\\m=(7)/(14)=0.5\ in/min`

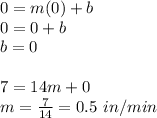
Therefore, the values of 'm' and 'b' are 0.5 and 0 respectively.

Thus, the linear model is given as:

`w=0.5t`