Question

Joanne and Karen run the 5000 feet from their house to the park. Karen sets off first, but runs 2.5 feet per minute slower than Joanne. The girls reach the park at the same time. If Karen takes 15 minutes to run to the park, how long does Joanne take?

Answer 1

It will take Joanna nearly the same time as Karen to run the park and time taken is 15 min and 7 seconds.

Explanation:

Let the time taken by Joanne be 'x' minutes.

Given:

Total distance traveled by both is,
`d=5000\ ft`

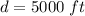
Speed of Karen is 2.5 feet per minute slower than Joanne's.

Time taken by Karen is,
`T_K=15\ min`

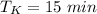
Now, speed of Karen is given as:

`S_K=(Distance)/(Time)\\S_K=(d)/(T_K)\\S_K=(5000)/(15)=(1000)/(3)\ ft/min`

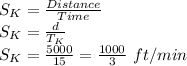
Now, as per question,

Speed of Karen = Speed of Joanne - 2.5

∴ Speed of Joanne = Speed of Karen + 2.5

`S_J=(1000)/(3)-2.5\\\\S_J=(1985)/(6)\ ft/min`

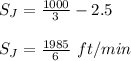
Now, we have speed of Joanne and distance traveled by Joanne. Therefore, time taken by Joanne is given as:

`x=(Distance)/(Speed)\\\\x=(d)/(S_J)\\\\x=5000/ (1985)/(6)\\\\x=5000* (6)/(1985)\\\\x=(5000* 6)/(1985)=15.11\ min\approx15\ min 7\ seconds`

Therefore, it will take Joanna nearly the same time to run the park and time taken is 15 min and 7 seconds.