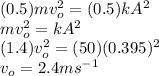Question

A 1.4-kg cart is attached to a horizontal spring for which the spring constant is 50 N/m . The system is set in motion when the cart is 0.21 m from its equilibrium position, and the initial velocity is 2.0 m/s directed away from the equilibrium position.Part A. What is the amplitude of the oscillation?Part B. What is the speed of the cart at its equilibrium position?

Answer 1

(a) 0.4 m

(b) 2.392 m/s

Step-by-step explanation:

mass, m = 1.4 kg

spring constant, k = 50 N/m

x = 0.21 m

velocity maximum, v = 2 m/s

(A) Angular frequency,
`\omega =\sqrt{(K)/(m)}`

`\omega =\sqrt{(50)/(1.4)}`

ω = 5.98 rad/s

(a) Let amplitude is A.

`v=\omega \sqrt{A^(2)-x^(2)}`

`2=5.98 \sqrt{A^(2)-0.21^(2)}`

0.1119 = A² - 0.0441

A = 0.4 m

(b) At the equilibrium position, the speed is maximum

maximum speed, v = ωA = 5.98 x 0.4 = 2.392 m/s

Answer 2

A)

0.395 m

B)

2.4 m/s

Step-by-step explanation:

A)

`m` = mass of the cart = 1.4 kg

`k` = spring constant of the spring = 50 Nm⁻¹

`x` = initial position of spring from equilibrium position = 0.21 m

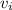`v_(i)` = initial speed of the cart = 2.0 ms⁻¹

`A` = amplitude of the oscillation = ?

Using conservation of energy

Final spring energy = initial kinetic energy + initial spring energy

`(0.5) kA^(2) = (0.5) m v_(i)^(2) + (0.5) k x_(i)^(2) \\kA^(2) = m v_(i)^(2) + k x_(i)^(2) \\(50) A^(2) = (1.4) (2.0)^(2) + (50) (0.21)^(2) \\A = 0.395 m`

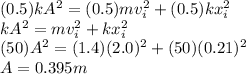
B)

`m` = mass of the cart = 1.4 kg

`k` = spring constant of the spring = 50 Nm⁻¹

`A` = amplitude of the oscillation = 0.395 m

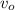`v_(o)` = maximum speed at the equilibrium position

Using conservation of energy

Kinetic energy at equilibrium position = maximum spring potential energy at extreme stretch of the spring

`(0.5) m v_(o)^(2) = (0.5) kA^(2)\\m v_(o)^(2) = kA^(2)\\(1.4) v_(o)^(2) = (50) (0.395)^(2)\\v_(o) = 2.4 ms^(-1)`