Answer:
Explanation:
Given that according to a study of the power quality (sags and swells) of a transformer, for transformers built for heavy industry, the distribution of the number of sags per week has a mean of 360 with a standard deviation of 108
Sample size n =216
By central limit theorem we have sample mean will follow a normal distribution with mean=360 and std deviation =
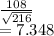
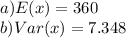
c) Bell shaped
d) P(X>414) = 0.0000
(almost uncertain event)