Question

A double-slit arrangement produces bright interference fringes for sodium light ( λ = 603 nm) that are angularly separated by 0.49° near the center of the pattern. What is the angular fringe separation if the entire arrangement is immersed in water, which has an index of refraction of 1.33?

Answer 1

θ for water = 0.3684°

Step-by-step explanation:

given data

wavelength λ = 603 nm

angle θ = 0.49°

index of refraction n = 1.33

to find out

angular fringe separation

solution

we know that double slit interference is here

m λ = d sin(θ) .................1

so for air it will be

m λ(air) = d sin(θ)air ...........2

and for water it will be

m λ(water) = d sin(θ)water .............3

now we take here ratio of equation 2 and 3

`(\lambda (water))/(\lambda(air))` =
`(sin(\Theta)water)/(sin(\Theta)air)`

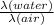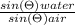
and

ratio of wavelength is =
`(1)/(n)`

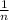
ratio of wavelength =
`(1)/(1.33)`

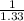
ratio of wavelength = 0.75187

so

sin(θ)water = sin(θ)air (0.75187)

sin(θ)water = sin(0.49) (0.75187)

sin(θ)water = 0.006429

so (θ)water is

(θ)water = 0.3683°

we notice here that by using small angle formula

we have approximate sin(θ) = θ

so θ for water is =
`(\Theta )/(n)`

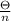
θ for water =
`(0.49)/(1.33)`

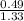
θ for water = 0.3684°