Question

In a study of computer use, 1000 randomly selected Canadian Internet users were asked how much time they spend using the Internet in a typical week (Ipsos Reid, August 9, 2005). The mean of the sample observations was 12.7 hours.

a. The sample standard deviation was not reported, but suppose that it was 5 hours. Carry out a hypothesis test with a significance level of .05 to decide if there is convincing evidence that the mean time spent using the Internet by Canadians is greater than 12.5 hours.
b. Now suppose that the sample standard deviation was 2 hours. Carry out a hypothesis test with a significance level of 0.05 to decide if there is convincing evidence that the mean time spent using the Internet by Canadians is greater than 12.5 hours.
c. Explain why the null hypothesis was rejected in the test of Part (b) but not in the test of Part (a).

Answer 1

Explanation:

Given that in a study of computer use, 1000 randomly selected Canadian Internet users were asked how much time they spend using the Internet in a typical week (Ipsos Reid, August 9, 2005). The mean of the sample observations was 12.7 hours.

a)
`H_0: \bar x =12.5\\H_a: \bar x >12.5`

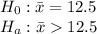
(right tailed test at 5% level)

`\sigma = 5\\std error = (5)/(√(1000) ) \\=0.158`

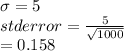
test statistic Z = Mean diff/std error = 1.265

(Here z test is used because sigma is known)

p value = 0.103

Since p >0.05, we accept H0

b) Here s= 2 hours.

But sample size is very large so z test is used.

Std error =
`(2)/(√(1000) ) \\=0.0632`

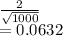
Test statistic = 3.16

p value =0.000783

since p <alpha, H0 is rejected

c) Because std deviation was less in part B, we got p value very low thus making us reject H0 in part B.