Question

Which expression is equivalent to cot t sec t?

A.
csc t
B.
sin t
C.
tan t
D.
sin2 t
E.
csc2 t

Answer 1

Answer:
`csc(t)`

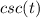
Explanation:

Alright, lets get started.

The given expression is given as :

`cot( t) * sec (t)`

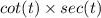
We know quotient identity as :

`cot(t)=(cos(t))/(sin(t))`

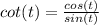
Similarly, we know reciprocal identity as :

`sec(t)=(1)/(cos(t))`

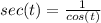
lets plug the value of cot and sec in given expression

`(cos(t))/(sin(t))  * (1)/(cos(t))`

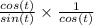
cos will be cancelled, remaining will be

`(1)/(sin(t))`

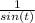
Using reciprocal identity again, that will equal to :

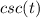`csc(t)` ................... Answer (A)