Question

Because of your expert physics skills, you have been hired as an analyst in a court case involving an automobile accident. The accident involved a 3,000 kg car (car A) which approached a stationary car of mass 1,841 kg (car B). The driver of car A slammed on his brakes(locking his wheels) 14 m before he/she crashed into car B. After the collision, car A slid 19 m forward while car B slid 26 m forward (Note: the cars did not stick together upon colliding). The coefficient of kinetic friction between the locked wheels and the road was measured to be 0.8. Calculate the speed of car A, in mph, at the moment he began braking. (1 mph

Answer 1

v = 91.8 Km / h

Step-by-step explanation:

We must start this exercise at the end, let's look for the lighter car acceleration (B), for this we use Newton's second law

fr = m a

a = fr / m

fr = μ N

N-W = 0

Let's replace

a = μ m g / m

a = μ g

a = 0.8 9.8

a = 7.84 m / s²

As the car B after the crash reached an initial velocity vo₀₂ and at the end of the fine speed zero, let us use kinematics

v² = v₀₂² - 2 a x

0 = v₀₂² - 2 a x

v₀₂ = 2 a x₂

v₀₂ = √ (2 7.84 26)

v₀₂ = 20.19 m / s

Let's perform the same procedure for car A, the acceleration is the same as it does not depend on the mass of the vehicles

v₀₁ = √ 2 a x₁

v₀₁ = √ (2 7.84 19)

v₀₂ = 17.36 m / s

Now let's use moment conservation, where the system is the two vehicles

Initial before crash.

p₀ = M v₁ + 0

After the crash

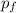`p_(f)` = M v₀₁ + m v₀₂

p₀ =
`p_(f)`

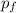
M v₁ = M v₀₁ + m v₀₂

v₁ = v₀₁ + m / M v₀₂

v₁ = 17.36 + 1841/3000 20.19

v₁ = 20.75 m / s

This is the speed of car 1 (A) just before the crash, now let's look for the speed when I apply the brakes the initial speed (v)

v₁² = v² - 2 a x₁

v = √ (v₁² + 2 a x₁)

v = √ (20.75² + 2 7.84 14)

v = 25.50 m / s

v = 25.50 m / s (1km / 1000m) (3600s / 1h)

v = 91.8 Km / h