Question

A small logo is embedded in a thick block of crown glass (n = 1.52), 4.70 cm beneath the top surface of the glass. The block is put under water, so there is 1.70 cm of water above the top surface of the block. The logo is viewed from directly above by an observer in air. How far beneath the top surface of the water does the logo appear to be?

Answer 1

The concept required to solve this problem is the optical relationship that exists between the apparent depth and actual or actual depth. This is mathematically expressed under the equations.

`d'w = d_w ((n_(air))/(n_w))+d_g ((n_(air))/(n_g))`

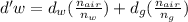
Where,

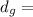`d_g =` Depth of glass

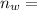`n_w =` Refraction index of water

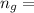`n_g =` Refraction index of glass

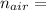`n_(air) =` Refraction index of air

`d_w =` Depth of water

I enclose a diagram for a better understanding of the problem, in this way we can determine that the apparent depth in the water of the logo would be subject to

`d'w = d_w ((n_(air))/(n_w))+d_g ((n_(air))/(n_g))`

`d'w = (1.7cm) ((1)/(1.33))+(4.2cm)((1)/(1.52))`

`d'w = 4.041cm`

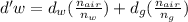
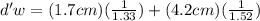
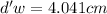
Therefore the distance below the upper surface of the water that appears to be the logo is 4.041cm