Question

You are designing a manned submersible to withstand the pressure of seawater at the bottom of the Mariana Trench, which is one of the deepest parts of the earth’s oceans. The bottom of the trench is at a depth of 10,900 m.Part A What is the gauge pressure at this depth? (You can ignore the small changes in the density of the water with depth.)Part B What is the inward force on a circular glass window 6.0 cm in diameter due to the water outside?Part C If the internal pressure is 1 atm, what outward force does this produce on the window? (You may ignore the small variation in pressure over the surface of the window.)

Answer 1

110029941 Pa

311388.81857 N

286.48968 N

Step-by-step explanation:

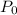`P_0` = Atmospheric pressure = 101325 Pa

`\rho` = Density of seawater = 1029 kg/m³

h = Depth = 10900 m

g = Acceleration due to gravity = 9.81 m/s²

r = Radius = 3 cm

A = Area =
`\pi r^2`

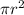
Gauge pressure

`P_g=\rho gh\\\Rightarrow P_g=1029* 9.81* 10900\\\Rightarrow P_g=110029941\ Pa`

The gauge pressure is 110029941 Pa

Net pressure at the given depth

`P=P_0+\rho gh\\\Rightarrow P=101325+1029* 9.81* 10900\\\Rightarrow P=110131266\ Pa`

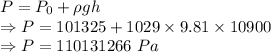
Force is given by

`F=PA\\\Rightarrow F=110131266* \pi 0.03^2\\\Rightarrow F=311388.81857\ N`

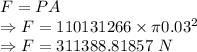
The force is 311388.81857 N

Now if P = 1 atm

`F=101325* \pi 0.03^2\\\Rightarrow F=286.48968\ N`

The force is 286.48968 N