Answer:
(a)
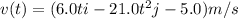
(b)

(c)
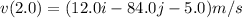
(d)
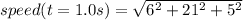 = 22.41 m/s;
= 22.41 m/s;
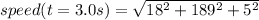 = 189.92 m/s
= 189.92 m/s
(e) average velocity = (9i-21j-5) m/s
Step-by-step explanation:
For the given problem:

(a) The velocity as a function of time: v(t) = dr/dt. Thus:
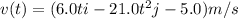
(b) The acceleration as a function of time: a(t) = dv/dt. Thus:

(c) The particle velocity at t= 2.0s. Using the equation in part (a);
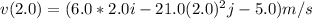
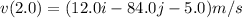
(d) Its speed at t=1.0s and t=3.0s
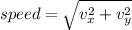
at t=1.0s
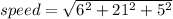 = 22.41 m/s
= 22.41 m/s
at t= 3.0s
 = 189.92 m/s
= 189.92 m/s
(e) The average velocity between t = 1.0 s and t = 2.0 s. Using the equation for r(t).
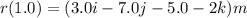 m
m
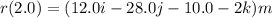
average velocity = Δr/Δt = (r2-r1)/(t2-t1) = (9i-21j-5) m/s