Question

A store sells both cold and hot beverages. Cold beverages, LaTeX: cc, cost $1.50, while hot beverages, LaTeX: hh, cost $2.00. On Saturday, drink receipts totaled $360, and 4 times as many cold beverages were sold as hot beverages. Part 1: Write a system of equations to represent the beverage sales on Saturday.

Answer 1

The system of equations which represents the beverage sales on Saturday are
`\left \{ {{1.5c+2h=360} \atop {c=4h}} \right.`

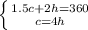
On Saturday 45 Hot beverages and 180 Cold beverages were sold.

Explanation:

Given:

Cost of Cold beverages = $1.50

Cost of Hot beverages = $2.00

Total drink receipts = $360.

Let the number of Cold beverages be c.

Also let number of Hot beverages be h.

Hence Total drink receipts is equal to sum of Cost of Cold beverages multiplied by number of cold beverages and Cost of Hot beverages multiplied by number of Hot beverages.

Framing in equation form we get;

`1.5c+2h=360 \ \ \ \ eqaution \ 1`

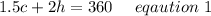
Also Given:

On Saturday, 4 times as many cold beverages were sold as hot beverages.

`c=4h \ \ \ \ equation \ 2`

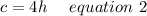
Hence the system of equations which represents the beverage sales on Saturday are
`\left \{ {{1.5c+2h=360} \atop {c=4h}} \right.`

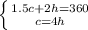
Now solving the equations we get;

Substituting the equation 2 in equation 1 we get;

`1.5c+2h=360\\1.5(4h)+2h=360\\6h+2h= 360\\8h=360\\h=(360)/(8)=45`

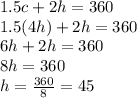
Now substituting the value of h in equation 2 we get;

`c=4h\\c=4*45 = 180`

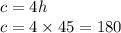
Hence On Saturday 45 Hot beverages and 180 Cold beverages were sold.