Answer:
Option A
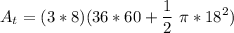
Explanation:
Area of compound figures
When we fid a compound shape, we must try to break it down into two standard shapes, find their areas using formulas and then add them to compute the final area.
The image provided in the question corresponds to a semi-circle on top of a rectangle. All the dimensions are given, so we can compute the area of each part of the window, add them to find the total area of the window, and finally multiply it by the total number of windows that were insulated with a glaze.
The area of a rectangle of dimensions X,Y is
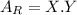
Our window has dimensions 36 in by 60 in, so
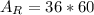
The top of the window is half a circle, which area is computed as
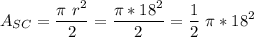
The total of each window is the sum of the above
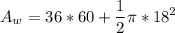
The hotel's grand dining room has three walls facing the gardens, each of which contains 8 insulated windows. The total area of the windows is (3*8) times the area of each window
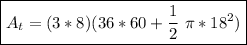
This result corresponds to the option A