Question

Mrs. Hill is preparing for group art projects. She has 52 pipe cleaners, 78 pieces of colored paper, 91 cotton balls and 117 pieces of yarn. Each group will get the same number of each ind of art supply. What is the greatest number of groups she can make if all the supplies are used? How many of each item will be in each group?

Answer 1

Greatest number of groups she can make is 13.

Each group will have 4 pipe cleaners, 6 pieces of colored paper, 7 cotton balls and 9 pieces of yarn.

Explanation:

Given:

Number of pipe cleaners = 52

Number of colored paper pieces = 78

Number of cotton balls = 91

Number of pieces of yarn = 117

Each group getting the same number of each type of given supplies.

Now, in order to get the greatest the number of groups to make so that each get same supply is given by the GCF (Greatest Common Factor) of all the individual types of supplies.

Therefore, let us write the factors of each type in terms of its prime factors.

52 = 13, 2

78 = 2, 3, 13

91 = 7, 13

117 = 3, 13

Therefore, the GCF is 13. So, maximum number of groups = 13.

Now, there are 52 pipe cleaners. Dividing 52 into 13, each will get:

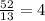`(52)/(13)=4` pipe cleaners

There are 78 colored paper pieces. Dividing 78 into 13, each will get:

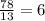`(78)/(13)=6` colored paper pieces.

There are 91 cotton balls. Dividing 91 into 13, each will get:

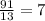`(91)/(13)=7` cotton balls.

There are 117 pieces of yarn. Dividing 117 into 13, each will get:

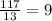`(117)/(13)=9` pieces of yarn.

Therefore, each group will have 4 pipe cleaners, 6 pieces of colored paper, 7 cotton balls and 9 pieces of yarn.