The equation for the line that passes through the point (1,-3) and that is parallel to the line with the equation
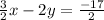 is:
is:

Solution:
Given that line that passes through the point (1, -3) and that is parallel to the line with the equation
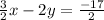
We have to find equation of line
The slope intercept form is given as:
y = mx + c
Where "m" is the slope of line and "c" is the y-intercept
Let us first find slope of line containing equation
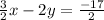
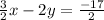
Rearrange the above equation into slope intercept form
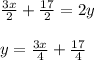
On comparing the above equation with slope intercept form y = mx + c,
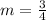
So the slope of line containing equation
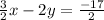 is
is
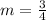
We know that slopes of parallel lines are equal
So the slope of line parallel to line having above equation is also
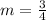
Now let us find the equation of line having slope m = 3/4 and passes through point (1 , -3)
Substitute
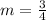 and (x, y) = (1 , -3) in slope intercept form
and (x, y) = (1 , -3) in slope intercept form
y = mx + c
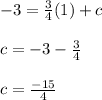
Thus the required equation of line is:
substitute
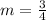 and
and
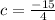 in slope intercept form
in slope intercept form
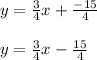
Thus the equation of line is found out