Question

Test the given claim. Identify the null​ hypothesis, alternative​ hypothesis, test​ statistic, P-value, and then state the conclusion about the null​ hypothesis, as well as the final conclusion that addresses the original claim. Among 21422142 passenger cars in a particular​ region, 239239 had only rear license plates. Among 399399 commercial​ trucks, 5454 had only rear license plates. A reasonable hypothesis is that commercial trucks owners violate laws requiring front license plates at a higher rate than owners of passenger cars. Use a 0.050.05 significance level to test that hypothesis. a. Test the claim using a hypothesis test. b. Test the claim by constructing an appropriate confidence interval.

Answer 1

a) Failed to reject the null hypothesis (P-value=0.09).

b) The 95% CI for the difference in proportions is:

`-0.0599\leq\pi_1-\pi_2\leq0.0124`

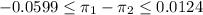
Explanation:

a) We have to perform a hypothesis test for the difference of proportions.

The null and alternative hypothesis are:

`H_0: \pi_1\geq\pi_2\\\\H_1: \pi_1<\pi_2`

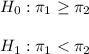
The significance level is 0.05.

The proportion of the passenger cars owners is:

`p_1=(239)/(2142) =0.1116`

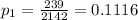
The proportion of commercial truck owners is:

`p_2=(54)/(399)=0.1353`

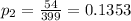
The weigthed average p is

`p=(n_1p_1+n_2p_2)/(n_1+n_2)=(239+54)/(2142+399)=0.1153`

The estimated standard deviation is

`s=\sqrt{(p(1-p))/(n_1)+(p(1-p))/(n_2)} =\sqrt{(0.1153(1-0.1153))/(2142)+(0.1153(1-0.1153))/(399)} =0.0174`

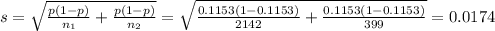
We can calculate the z-value as:

`z=(\Delta p)/(s)=(0.1116-0.1353)/(0.0174)=-1.362`

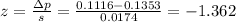
The P-value for z=-1.362 is P=0.0866.

The P-value (0.09) is greater than the significance level (0.05), so it failed to reject the null hypothesis. There is no enough evidence to prove that commercial trucks owners violate laws requiring front license plates at a higher rate than owners of passenger cars.

b) We can construct a 95% CI, according to the significance level of 0.05.

The z-value for this CI is 1.96.

We have to recalculate the standard deviation:

`\sigma=\sqrt{(p_1(1-p_1))/(n_1) +(p_2(1-p_2))/(n_2)} =\sqrt{(0.1116(1-0.1116))/(2142) +(0.1353(1-0.1353))/(399)} =0.0184`

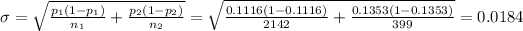
The lower limit is then:

`LL=(p_1-p_2)-z*\sigma=(0.1116-0.1353)-1.96*0.0184=-0.0238-0.0361\\\\LL=-0.0599`

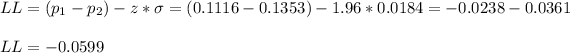
The upper limit is:

`UL=(p_1-p_2)+z*\sigma=(0.1116-0.1353)+1.96*0.0184=-0.0238+0.0361\\\\UL=0.0124`

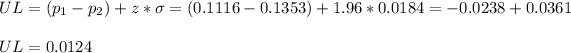
The 95% CI for the difference in proportions is:

`-0.0599\leq\pi_1-\pi_2\leq0.0124`

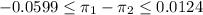
In this case, we can conclude that the difference between the proportions, with 95% confidence, can still be equal or greater than zero, meaning that it is possible passenger car owners violate laws more than truck owners.