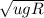Question

A curve in a stretch of highway has radius R. The road is not banked in any way. The coefficient of static friction between the tires and the road is . What is the fastest speed that a car can safely travel around the curve

Answer 1

maximum possible velocity =
`√(ugR)`

Step-by-step explanation:

centripetal acceleration when the car is going in the circle must be less than the maximum friction for the car to not slip.

centripetal acceleration
`(mv^(2))/(r)`

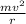
where v is the velocity of car and r is the radius of circle

maximum friction = umg

where u is the coefficient of static friction.

therefore
`umg\geq (mv^(2))/(R)`

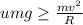
therefore maximum possible velocity =
`√(ugR)`