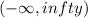Question

Find the Taylor series for f(x)=sin(x) centered at c=π/2.sin(x)=∑ n=0 [infinity]On what interval is the expansion valid? Give your answer using interval notation.

Answer 1

sinx =1-\frac{1}{2} (x-\frac{\pi}{2} )^2+\frac{1}{24} (x-\frac{\pi}{2} )^4-\frac{1}{720} (x-\frac{\pi}{2} )^6+\frac{1}{40320} (x-\frac{\pi}{2} )^8+...

Explanation:

given that f(x) = sin x

we have to find the Taylor series for that

`f(x) = sin x   : f( = 1\\f'(x) = cos x :(f'(\pi)/(2))=0\\f`

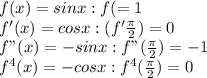
and so on.

i.e. 2nd, 4th, 6th terms would be 0

and also 1st, 5th, 9th terms would be positive for f value and 3rd, 9th,... would be negative

Using the above we can write Taylor series as

`f(x) = f(a)+(f'(a))/(1!) (x-(\pi)/(2)) +...+f^n(a) /n! (x- (\pi)/(2))^n+...`

`sinx =1-(1)/(2) (x-(\pi)/(2) )^2+(1)/(24) (x-(\pi)/(2) )^4-(1)/(720) (x-(\pi)/(2) )^6+(1)/(40320) (x-(\pi)/(2) )^8+...`

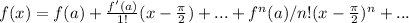
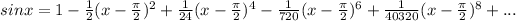
This is valid for all real values of x.

x ∈
`(-\infty, infty)`