Question

An article in the Journal of Aircraft (Vol. 23, 1986, pp.859–864) described a new equivalentplate analysis method formulation that is capable of modelingaircraft structures such as cranked wingboxes and that produces results similar to the more computationallyintensive finite element analysismethod. Natural vibration frequencies for the cranked wing boxstructure are calculated using bothmethods, and results for the first seven natural frequenciesfollow:Freq. Finite Element Cycle/s Equivalent Plate, Cycle/s

1 14.58 14.762 48.52 49.103 97.22 99.994 113.99 117.535 174.73 181.226 212.72 220.147 277.38 294.80
a. Do the data suggest that the two methods provide the same meanvalue for natural vibrationfrequency? Use α = 0.05. Find the P-value.b. Find a 95% confidence interval on the mean difference betweenthe two methods.

Answer 1

a)
`t=\frac{(134.163 -139.649)-(0)}{\sqrt{(92.857^2)/(7)+(98.435^2)/(7)}}=-0.107`

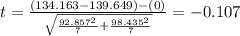
Now we can calculate the degrees of freedom given by:

`df=7+7-2=12`

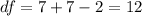
And now we can calculate the p value using the altenative hypothesis:

`p_v =2*P(t_(14)<-0.107) =0.917`

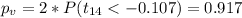
b) The 95% confidence interval would be given by
`-116.986 \leq \mu_1 -\mu_2 \leq 106.014`

Explanation:

Data given

Freq. Finite Element Cycle/s Equivalent Plate, Cycle/s

_____________________________________________

1 14.58 14.76

2 48.52 49.10

3 97.22 99.99

4 113.99 117.53

5 174.73 181.22

6 212.72 220.14

7 277.38 294.80

_____________________________________________

The system of hypothesis on this case are:

Null hypothesis:
`\mu_1 = \mu_2`

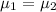
Alternative hypothesis:
`\mu_1 \\eq \mu_2`

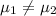
Or equivalently:

Null hypothesis:
`\mu_1 - \mu_2 = 0`

Alternative hypothesis:
`\mu_1 -\mu_2\\eq 0`

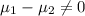
Our notation on this case :

`n_1 =7` represent the sample size for group 1 ( Finite Element_

`n_2 =7` represent the sample size for group 2 (Equivalent Plate)

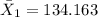`\bar X_1 =134.163` represent the sample mean for the group 1 ( Finite Element)

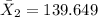`\bar X_2 =139.649` represent the sample mean for the group 2 (Equivalent Plate)

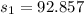`s_1=92.857` represent the sample standard deviation for group 1 ( Finite Element)

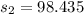`s_2=98.435` represent the sample standard deviation for group 2 (Equivalent Plate)

a. Do the data suggest that the two methods provide the same meanvalue for natural vibrationfrequency? Use α = 0.05. Find the P-value.

And the statistic is given by this formula:

`t=\frac{(\bar X_1 -\bar X_2)-(\mu_(1)-\mu_2)}{\sqrt{(s^2_1)/(n_1)+(s^2_2)/(n_2)}}`

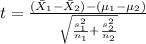
And now we can calculate the statistic:

`t=\frac{(134.163 -139.649)-(0)}{\sqrt{(92.857^2)/(7)+(98.435^2)/(7)}}=-0.107`

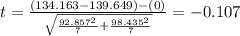
Now we can calculate the degrees of freedom given by:

`df=7+7-2=12`

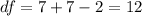
And now we can calculate the p value using the altenative hypothesis:

`p_v =2*P(t_(14)<-0.107) =0.917`

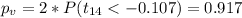
So with the p value obtained and using the significance level given
`\alpha=0.05` we have
`p_v>\alpha` so we can conclude that we have enough evidence to FAIL to reject the null hypothesis, and we can said that at 5% of significance that difference of means is not different from 0.

b. Find a 95% confidence interval on the mean difference between the two methods

The confidence interval for the difference of means is given by the following formula:

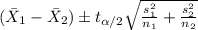`(\bar X_1 -\bar X_2) \pm t_(\alpha/2)\sqrt{(s^2_1)/(n_1)+(s^2_2)/(n_2)}` (1)

The point of estimate for
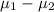`\mu_1 -\mu_2` is just given by:

`\bar X_1 -\bar X_2 =134.163-139.649=-5.486`

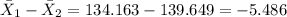
In order to calculate the critical value
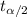`t_(\alpha/2)` we need to find first the degrees of freedom, given by:

`df=n_1 +n_2 -1=7+7-2=12`

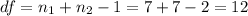
Since the Confidence is 0.95 or 95%, the value of
`\alpha=0.05` and
`\alpha/2 =0.025`, and we can use excel, a calculator or a table to find the critical value. The excel command would be: "=-T.INV(0.025,12)".And we see that
`t_(\alpha/2)=2.18`

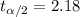
Now we have everything in order to replace into formula (1):

`-5.486-2.18\sqrt{(92.857^2)/(7)+(98.435^2)/(7)}=-116.986`

`-5.486+2.18\sqrt{(92.857^2)/(7)+(98.435^2)/(7)}=106.014`

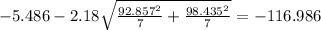
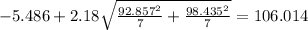
So on this case the 95% confidence interval would be given by
`-116.986 \leq \mu_1 -\mu_2 \leq 106.014`