Question

Choose two positive integers a and b, making sure that a<5 and b>80 . The width of a rectangular computer screen is a inches more than its height. If the area of the screen is is b square inches, determine the dimensions of the computer screen.

Answer 1

Dimensions of the screen are a minimum of 10 inches wide by 8 inches high. The difference between the height and width will be 2 inches

Explanation:

`Height = H`

`Width = H + a`

`Area = Height x Width`

`b = H * (H + a)`

`b = H^(2) + aH`

`H^(2) + aH > 80`

`H^(2) + aH - 80 > 0`

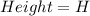
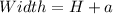
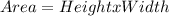
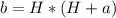
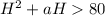
a<5 means 'a' can be a = 1, 2, 3, 4

Solving for H for each option of 'a' will give values of 'H' using the quadratic formula below

`H = \frac{-b\±\sqrt{b^(2)-4ac}}{2a}`

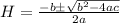
As 'a' and 'b' must be positive integers, H and W must be positive integers as well,

`a = 1, H = 8.46, H = -9.46`

`a = 2, H = 8, H = -10`

`a = 3, H = 7.57, H = -10.57`

`a = 4, H = 7.17, H = -11.17`

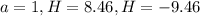
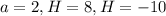
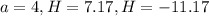
Based on above possible answers:

`a=2, H=8`

`W = H + a`

`W = 8 + 2`

`W = 10`

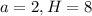
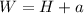
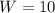
Dimensions of the screen are a minimum of 10 inches wide by 8 inches high. The difference between the height and width will be 2 inches