Answer:
a)
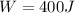
b)
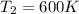
c)
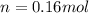
d)
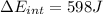
e)
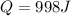
Step-by-step explanation:
a) Let's recall the definition of work.
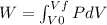
Because the system is a quasi-static isobaric expansion, P is constant here, therefore:
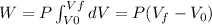
![W=2.0\cdot 10^(5)(4.0\cdot 10^(-3)-2.0\cdot 10^(-3))= 400 [Nm^(2)]](https://img.qammunity.org/2020/formulas/physics/college/7kfa9zygldmhx7wnovmj7h0c6mk80gjt30.png)
b) Using the ideal gas equation we have:
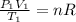 (1)
(1)
and
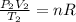 (2)
(2)
We can note that n times R is a constant in (1) and (2), so we can equal those equations.
 (3)
(3)
Let's solve T₂ for (3), let's recall that P₁ = P₂, so they canceled out
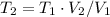
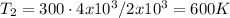
c) Using the equation of ideal gas we have:
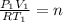

d) We can write the internal energy as a function of Cv, and as we know the Cv is 1.5R for a monoatomic gas.
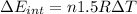
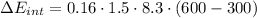
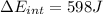
e) Using the first law of thermodynamic, we have:
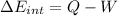
Finally,
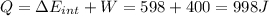
Have a nice day!