Question

5) What is the net force caused by the moon acting on earth when the moon is 3.86x10^8 m away? The moon has a mass of 7.46x10^23 kg.

6) what is the force due to gravity exerted by Jupiter on the planet Venus?
7) How much does the mass of Saturn pull Mars?
8) how much more is earths force of gravity on Pluto than Venus force of gravity on Pluto?

Thanks!

Answer 1

Answers:

5)
`1.99(10)^(21) N`

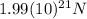
6)
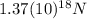
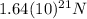
`1.37(10)^(18) N`

7)
`1.64(10)^(21) N`

8)
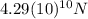`4.29(10)^(10) N` more than Venus force of gravity on Pluto

Step-by-step explanation:

According to Newton's law of Universal Gravitation, the force
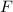`F` exerted between two bodies of masses
`M` and
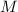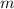`m` and separated by a distance
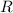`R` is equal to the product of their masses and inversely proportional to the square of the distance:

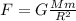`F=G(Mm)/(R^(2))` (1)

Where
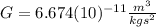`G=6.674(10)^(-11)(m^(3))/(kgs^(2))` is the Gravitational Constant

This is the equation we will use to solve each question in this problem.

5) Gravitational force between Earth and Moon

In this case we have:

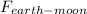`F_(earth-moon)` is the gravitational force between Earth and Moon

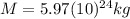`M=5.97(10)^(24) kg` is the mass of the Earth

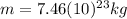`m=7.46(10)^(23) kg` is the mass of the Moon

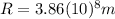`R=3.86(10)^(8) m` is the distance between Earth and Moon

Solving:

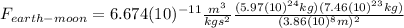`F_(earth-moon)=6.674(10)^(-11)(m^(3))/(kgs^(2))((5.97(10)^(24) kg)(7.46(10)^(23) kg))/((3.86(10)^(8) m)^(2))` (2)

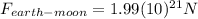`F_(earth-moon)=1.99(10)^(21) N` (3)

6) Gravitational force between Jupiter and Venus

Assuming for a moment that the planets are perfectly aligned and all are in the same orbital period, we can make a rough estimation of the distance between Jupiter and Venus, knowing the distance of each to the Sun:

distance between Sun and Jupiter - distance between Sun and Venus=distance between Jupiter and Venus=
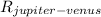`R_(jupiter-venus)` (4)

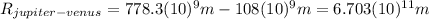`R_(jupiter-venus)=778.3(10)^(9) m - 108(10)^(9) m=6.703(10)^(11) m` (5)

Using this value in the Law of Universal Gravitation equation:

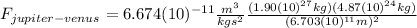`F_(jupiter-venus)=6.674(10)^(-11)(m^(3))/(kgs^(2))((1.90(10)^(27) kg)(4.87(10)^(24) kg))/((6.703(10)^(11) m)^(2))` (6)

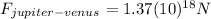`F_(jupiter-venus)=1.37(10)^(18) N` (7)

7) Gravitational force between Saturn and Mars

Using the same assumption we made in the prior question:

distance between Sun and Saturn - distance between Sun and Mars=distance between Saturn and Mars=
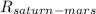`R_(saturn-mars)` (8)

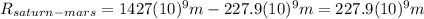`R_(saturn-mars)=1427(10)^(9) m - 227.9(10)^(9) m=227.9(10)^(9) m` (9)

Using this value in the Law of Universal Gravitation equation:

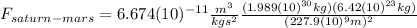`F_(saturn-mars)=6.674(10)^(-11)(m^(3))/(kgs^(2))((1.989(10)^(30) kg)(6.42(10)^(23) kg))/((227.9(10)^(9) m)^(2))` (10)

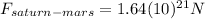`F_(saturn-mars)=1.64(10)^(21) N` (11)

8) How much more is earths force of gravity on Pluto than Venus force of gravity on Pluto?

Firstly, we need to find
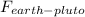`F_(earth-pluto)` and then find
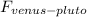`F_(venus-pluto)` in order to find the difference.

For
`F_(earth-pluto)`:

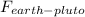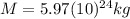`M=5.97(10)^(24) kg` is the mass of the Earth

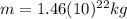`m=1.46(10)^(22) kg` is the mass of Pluto

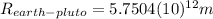`R_(earth-pluto)=5.7504(10)^(12) m` is the distance between Earth and Pluto

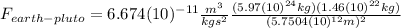`F_(earth-pluto)=6.674(10)^(-11)(m^(3))/(kgs^(2))((5.97(10)^(24) kg)(1.46(10)^(22) kg))/((5.7504(10)^(12) m)^(2))` (12)

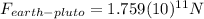`F_(earth-pluto)=1.759(10)^(11) N` (13) Force between Earth and Pluto

For
`F_(venus-pluto)`:

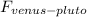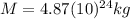`M=4.87(10)^(24) kg` is the mass of Venus

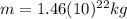`m=1.46(10)^(22) kg` is the mass of Pluto

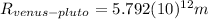`R_(venus-pluto)=5.792(10)^(12) m` is the distance between Venus and Pluto

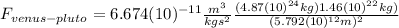`F_(venus-pluto)=6.674(10)^(-11)(m^(3))/(kgs^(2))((4.87(10)^(24) kg)1.46(10)^(22) kg))/((5.792(10)^(12) m)^(2))` (14)

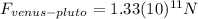`F_(venus-pluto)=1.33(10)^(11) N` (15) Force between Venus and Pluto

Calculating the difference:

`F_(earth-pluto)-F_(venus-pluto)=1.759(10)^(11) N-1.33(10)^(11) N`

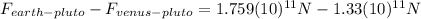
Finally:

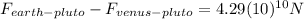`F_(earth-pluto)-F_(venus-pluto)=4.29(10)^(10) N` (16)

Hence:

Earths force of gravity on Pluto is
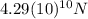`4.29(10)^(10) N` than Venus force of gravity on Pluto.