Question

Which of the following could be an example of a function with a range (-∞,a] and a domain [b, ∞) where a < 0 and b < 0?

a) f(x)=-\root(3)(x+a) -b

b) f(x)=-\root(3)((x+b)) -a

c) f(x)=-\sqrt(x-b)+ a

d) f(x)=-\sqrt(x-a)+ b

Answer 1

`f(x) = - √(x - b) + a`

Explanation:

We have to choose the function from the given options which have a range (-∞, a] and a domain [b,∞) where a < 0 and b < 0.

I think the function is
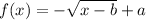`f(x) = - √(x - b) + a` ......... (1)

Here, x - b must be greater than equal to zero for the function to be real.

Hence, x - b ≥ 0

⇒ x ≥ b

So, the domain is [b, ∞).

Now, putting x = b in the equation (1),we get f(x) = a and putting x = ∞, we get f(x) = - ∞.

Therefore, the range of the function is (-∞, a]. (Answer)