Question

5. What is the probability that a number picked from the set {-4,-3,-2,-1,0,1,2,3,4,5) will be a

solution of 2x + 5> 1?
20%
30%
70%
80%

Answer 1

70%.

Explanation:

Rearrange the inequality to isolate
`x`. Start by subtracting
`5` from both sides of the inequality:

`2\,x + 5 - 5 > 1 - 5`,

`2\, x > -4`.

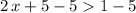Divide both sides by
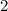`2`. (Keep in mind that if the multiplier or divisor is smaller than zero, it will flip the inequality sign.)

`x > -2`.

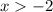There are ten numbers in this set. Only seven of them will satisfy this inequality. Note that the "
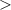`>`" symbol means strictly greater than (while "
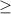`\ge`" means greater than or equal to.) As a result,
`x = -2` will not count as a solution.

Assume that the number is picked randomly.

`\begin{aligned}&\text{Probability of Success} \cr = & \frac{\text{Number of Choices that lead to Success}}{\text{Number of all Choices}} \cr =& (7)/(10) \cr = &0.7 \cr =& 70\% \end{aligned}`.