Question

Select all irrational numbers.

Answer 1

OPTION A

OPTION B

OPTION C

Explanation:

Irrational numbers are the subset of real numbers. Their decimal representation neither form a pattern nor terminate.

OPTION A:
`$ \sqrt{(1)/(2)} $`

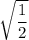
This is equal to
`$ (1)/(√(2)) $`.

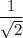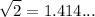`$ √(2) = 1.414... $` is non-terminating. So, it is an irrational number. Hence, the reciprocal of an irrational number would also be irrational. So, OPTION A is irrational.

OPTION B:
`$ \sqrt{(1)/(8)} $`

This is equal to
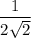`$ (1)/(2√(2)) $`. Using the same logic as Option A, we regard OPTION B to be irrational as well.

OPTION C:
`$ \sqrt{(1)/(10)} $`

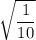
This is equal to
`$ (1)/(√(5)√(2)) $`.

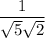Both
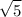`$ √(5) $` and
`$ √(2) $` are irrational. So, the product and the reciprocal of the product is irrational as well. So, OPTION C is an irrational number.

OPTION D:
`$ \sqrt{(1)/(16)} $`

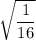
16 is a perfect square and is a rational number.
`$ (1)/(√(16)) $` =
`$ (1)/(4) $`. This is equal to 0.25, a terminating decimal. So, OPTION D is a rational number.

OPTION E:
`$ \sqrt{(1)/(4)} $`

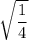
4 is a perfect square as well.
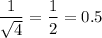`$ (1)/(√(4)) = (1)/(2) = 0.5 $`, a terminating decimal. So, OPTION E is a rational number.