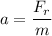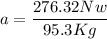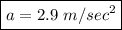Question

A student is swimming south applying a force of 256 N. The water exerts a westward force of 104 N. If the student has a mass of 95.3 kg, what is the acceleration of the student? Hint: the weight of the student is balanced with the water buoyant force, therefore those are the only forces affecting the resultant force.

Answer 1

`a=2.9\ m/sec^2`

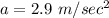
Step-by-step explanation:

Net Forces and Acceleration

The second Newton's Law relates the net force
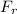`F_r` acting on an object of mass m with the acceleration a it gets. Both the net force and the acceleration are vector and have the same direction because they are proportional to each other.

`\vec F_r=m\vec a`

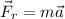
According to the information given in the question, two forces are acting on the swimming student: One of 256 N pointing to the south and other to the west of 104 N. Since those forces are not aligned, we must add them like vectors as shown in the figure below.

The magnitude of the resulting force
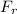`F_r` is computed as the hypotenuse of a right triangle

`|F_r|=√(256^2+104^2)`

`|F_r|=276.32\ Nw`

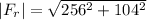
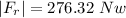
The acceleration can be obtained from the formula

`F_r=ma`

Note we are using only magnitudes here

`\displaystyle a=(F_r)/(m)`

`\displaystyle a=(276.32Nw)/(95.3Kg)`

`\boxed{a=2.9\ m/sec^2}`